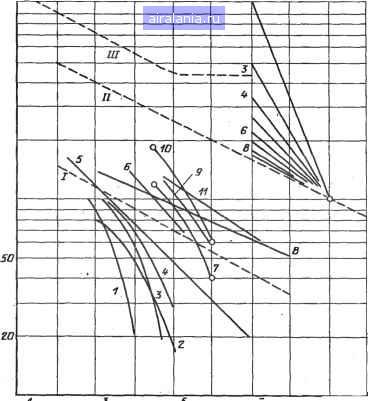10 10 10 10 10 Nf

Рие. 8.9. Зависимость числа циклов до отказа от ДГ:

7-симисторы ТС141-63,80 и ТС142-63,80; 2-оптотиристоры ТО2-40; 3-диоды Д131-50, Д131-63, Д131-80; <(-оптотиристоры ТО125-10 и Т0125-12,5; 5--шристоры [8,23, 8.33]; 6-тиристоры быстродействующие ТБ2-160, ТБЗ-200, ТБ-320, ТБ-400; 7-тиристоры Т161-125, Т161-160, Т171-200, Т171-250, TI7I-320; S-диоды [8.16]; 9-диоды ДЛ161-200, ДЛ 171-320; 70-диоды Д141-100-Д171-400; 77-тиристоры Т-630, Т-800, Т2-800, Т-1000; 7-[8.40]; 7/ -[8.41]; 777-[8.42]

На рис. 8.9 представлены результаты работ [8.16, 8.23, 8.33] и данные некоторых каталогов на СПП. В связи с TCNf что рис. 8.9 построен в логарифмических координатах (log А Г-log iVy), в случае, когда выполняется (8.6), зависимость

от А Г изображается прямой линией, в случае (8.7)-кривой. В работах [8.22, 8.34] предложены более сложные формулы, где число циклов до отказа зависит не только от AT, но и от ряда других факторов (например, от средней температуры структуры). Здесь мы не рекомендуем пользоваться этими более сложными формулами, так как входящие в них коэффициенты для большинства типов СПП неизвестны. На рис. 8.9 (вверху

справа) приведены прямые, наклон которых соответствует различным значениям параметра т (от 9 до 2). С помощью этих прямых можно определить наклон (т.е. значение т) для любой из приведенных на рис. 8.9 зависимостей.

Следует рассмотреть, как отказы в циклических режимах распределены во времени. Обычно для этого используют функцию плотности распределения f{N). В общем случае переход . от к г невозможен, поскольку циклы могут следовать нерегулярно во времени. Для f{N) известны две основные параметризации: логарифмически нормальная [8.10, 8.22, 8.35] и вейбулловская [8.23, 8.33]. Известна также работа [8.36], где при определении f{N) использовано дисперсионное распределение Бернштейна. Подчеркнем еще раз, что в большинстве работ рассматривались СПП с паяными контактами. Для современных мощных СПП прижимной конструкции можно указать лишь на работы [8.35, 8.37].

В [8.35] показано, что для тиристоров Т2-320 функция f{N) может быть описана логарифмически нормальным распределением с ненулевым параметром сдвига Nq. Значение Ло по данным [8.35] составило 2422 цикла для тиристоров, испытывавшихся при токе нагрузки 1200 А, и 8010 для тиристоров, испытывавшихся при токе 900 А. В [8.37] приведены данные, согласно которым приборы типа BSTR-15110 вьщерживают без отказов 10 млн. циклов при амплитуде перепада температуры структуры, равной 55° С. Там же указано, что таблеточные тиристоры с диаметром шайбы 25 мм без ухудшения параметров выдерживают 240000 циклов при ДТ=95°С (число испытанных приборов в [8.37] не приведено).

Теперь следует вернуться к формулам (8.6) и (8.7) и ответить на вопрос: какой характеристикой распределения является в этих формулах величина Np. Действительно, поскольку существует функция f{N), то в выражениях подобного типа необходимо обязательно указывать, что именно понимается под величиной N. среднее значение, медиана распределения или его мода. Несмотря на то что в большинстве работ под Nc понимают среднее значение [8.23 и jip.], в качестве ПН мы рекомендуем применять не а медиану

распределения-[8.3]. Причиной этого являются следующие обстоятельства. Во-первых, функция f{N) во многих случаях существенно асимметрична. При этом среднее значение оказывается плохим показателем, так как дает искаженное представление о циклостойкости изделий. Например, если f{N) соответствует логарифмически нормальному распределению, то ВБР для iV, = iV, при а =1,7 [8.10] составит 0,2 [i? (Л) = 0,2 ], т. е. такое число циклов выдержат всего лишь 20% СПП. Причиной этого оказывается увеличение за счет вклада

N=N=N

a) медиана N

Рис. 8.10. Соотношение между модой, медианой и средним значением для симметричного (о) и асимметричного (б) распределений. [Мода-значение, соответствующее максимуму f\bi). Медиана-значение, соответствующее ВБР, равной 50% (площадь слева от медианы равна площади справа). Среднее

значение- J /(Л) NdN\ о

(хотя и небольшого числа) очень стойких СПП. В то же время, если распределение близко к симметричному, то все равно, чем пользоваться в качестве ПН, так как среднее значение, медиана и мода близки между собой (на рис. 8.10 оба рассмотренных случая проиллюстрированы графически). Во-вторых, медиана в качестве ПН намного практичнее, чем среднее значение. Всамом деле, для определения и подтверждения величины надо довести до отказа все изделия, в том числе и самые стойкие. В то же время для определения и подтверждения величины надо довести до отказа лишь 50% приборов. Это может существенно уменьшить время, необходимое для испытаний на надежность.

Обращает на себя внимание малочисленность данных по циклостойкости СПП с прижимными контактами. Причиной этого является тот факт, что в связи с отказом от использования мягких припоев в конструкции СПП повысилась (см. выше) циклостойкость СПП на несколько порядков. Такое существенное улучшение данного ПН было принято изготовителями и разработчиками приборов за полное снятие проблемы, вследствие чего работы в этом направлении прекратились, а сам параметр даже не попал в число приводимых в технических условиях и каталогах. Между тем циклостойкость современных приборов хотя и велика, но небесконечна, и поэтому считать данную проблему решенной окончательно нельзя.

Рассмотрим режим импульсного циклирования. В более традиционной терминологии это тот режим, где существенна проблема ( «О-стойкости силовых тиристоров. Строго говоря, следует четко различать, о каком dildt идет речь. Дело в том, что когда рассматривают любое разрушающее воздействие, то существуют две возможные схемы для отказа прибора:

а) прибор может выйти из строя при однократном приложении данного воздействия;

б) прибор может выйти из строя при многократном приложении данного воздействия.