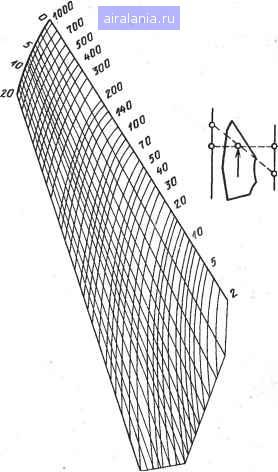Рис. 8.12. Номограмма и!

г- оро"!

-OfiZ

-0,05 -0,40

-цгс

-00 -0(tO

-оа -qfio

-0,70

-оро

-0,90

-ops

06 -09

XL-от

биномиального распределения Р{тс\ =

Как и следовало ожидать, значение точечной оценки и для ВБР, и для ИО находится внутри полученного интервала.

б) Так же как и в случае «а», из Р* = 0,9 следует Р*„ = Рв = 0,95. Номограммой в этом случае воспользоваться нельзя, так как п и J очень велики j[5000 и 475 соответственно). Вероятность отказа F, равная (1-i?), составляет 0,095. В связи

с тем что это значение меньше 0,1, хорошим приближением к биномиальному распределению явится распределение Пуассона [8.2], причем в качестве параметра ро этого распределения берется величина пР, т. е. ро = 475. Хотя уравнение Пуассона также табулировано почти во всех книгах по надежности, таблиц с таким большим значением io найти практически невозможно. Однако для Ро>30 распределение Пуассона можно заменить [8.2] на нормальное с параметрами р=475 и а=,Урл;21,8. Введем нормированную нормальную переменную:

x-\i х-415 21,8

Для нормированной переменной z находим по таблицам нормального распределения такое значение z, для которого Pr{zZi} = 0,05 (1-P*):zift;l,64. Из-за симметрии нормального распределения другой границе будет отвечать Z2=-1,64. Следовательно, имеем

Zi,2=±l,64=(x-475)/21,8,

откуда jcj;510,75 и л:2«439,25. Разделив полученные значения на и = 5000, находим нижнюю и верхнюю границы для вероятности отказа, откуда

„л;0,90 и RbKQ,9\.

Соответственно для ИО

£„ = 0,910-4/4 и £в=1-1о-Ч/ч,

т. е. окончательно

. Рг{0,910-М/ч<<1 • 10-Ч/ч} = 0,9.

Результаты расчета в случаях «а» и «б» показаны на рис. 8.13.

Перейдем к более сложной задаче - определению вида и параметров закона распределения отказов. Математики разработали ряд методов, позволяющих более или менее успешно решать эту задачу. С ними можно ознакомиться, например, в книге [8.53]. Ниже приведен лишь один метод

решения, а именно графичес- „

"1-. Рис. 8 13 Точечная оценка и довери-

кии. Его основным достоин- ,,,борок раз-

ством является то, что он личного объема (1-90%-ный дове-

позволяет отсеять формально рительный интервал)

Х-10*,1/ч

п=го

п=5000

Точечная оценка

0,94

. Ofi-I

aaas а,оаг ooai

Рис. 8.14. Нормальное распределение (ось абсцисс: равномерная ткала, а = 33 мм; ось ординат: шкала -функция Гаусса, );[Ф(1)] = 25 мм)

7J3t 190

о OB

« 6 в 10

« 5 eo(Zi-e

Рис. 8.15. Логарифмически нормальное распределение (ось абсцисс: шка.ча г логарифмическая, ,\: = 701g(f/f) мм; ось ординат: шкала-логарифмически нормальная, v [Ф (1)]=25 мм)

Правдоподобные, но по сути ошибочные решения. Идея графического метода заключается в том, что функция распределения отказов, отвечаюгцая определенному закону, в правильно подобранных масштабах по оси абсцисс и ординат изображается прямой линией. Выбор необходимых масштабов по осям означает построение соответствующей вероятностной бумаги. Бумага носит название того закона распределения, который изображается на ней прямой линией. На рис. 8.14- 8.16 приведены сетки вероятностной бумаги для нормального, логарифмически нормального и вейбулловского распределений. Следует иметь в виду, что прежде чем использовать готовую вероятностную бумагу, надо проанализировать имеющиеся 368